lucene系列(14)工具类之快速选择算法

lucene►util , , , 评论

前言

什么是选择算法？

在计算机科学中，选择算法是一种在列表或数组中找到第 k 个最小数字的算法；

计算集合中第 k 大（小）的元素。就是 topK 相关系列的问题，但是选择算法只需要找到第 k 个就好。

在 lucene 的源码中，对于选择算法定义了一个接口：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/** An implementation of a selection algorithm, ie. computing the k-th greatest
 *  value from a collection. */
// 选择算法，topK 问题
public abstract class Selector {

  /** Reorder elements so that the element at position {@code k} is the same
   *  as if all elements were sorted and all other elements are partitioned
   *  around it: {@code [from, k)} only contains elements that are less than
   *  or equal to {@code k} and {@code (k, to)} only contains elements that
   *  are greater than or equal to {@code k}. */
  // 重排序元素，以使 k 位置的元素作为分割点。from->k 的都是小于等于 k 的。k -> to 的都是大于 k 的
  public abstract void select(int from, int to, int k);

  void checkArgs(int from, int to, int k) {
    if (k < from) {
      throw new IllegalArgumentException("k must be >= from");
    }
    if (k >= to) {
      throw new IllegalArgumentException("k must be < to");
    }
  }

  /** Swap values at slots <code>i</code> and <code>j</code>. */
  // 交换两个槽的内容
  protected abstract void swap(int i, int j);
}

定义的接口除了选择还有交换。

Lucene 对于选择算法有两个实现，快速选择算法及基数选择算法。本文将详细分析快速选择算法的源码。该类的路径是：org.apache.lucene.util.IntroSelector.

完整版本的带有注释的源码在 github 上。IntroSelector 源码

原理介绍

在计算机科学中，快速选择（英语：Quickselect）是一种从无序列表找到第 k 小元素的选择算法。它从原理上来说与快速排序有关。与快速排序一样都由托尼·霍尔提出的，因而也被称为霍尔选择算法。[1] 同样地，它在实际应用是一种高效的算法，具有很好的平均时间复杂度，然而最坏时间复杂度则不理想。快速选择及其变种是实际应用中最常使用的高效选择算法。

快速选择的总体思路与快速排序一致，选择一个元素作为基准来对元素进行分区，将小于和大于基准的元素分在基准左边和右边的两个区域。不同的是，快速选择并不递归访问双边，而是只递归进入一边的元素中继续寻找。这降低了平均时间复杂度，从 O(n log n) 至 O(n)，不过最坏情况仍然是 O(n2)。

对于快速排序，想必大家对其原理都很清楚，这里不赘述了。

众所周知，快速排序最坏的时间复杂度是 O(n2). 快速选择也是。

最坏情况通常出现在每次选择分割点时，都选择了最错误的那个。比如在已排序数组中每次都取第一个，那么根本起不到分割的作用。

因此，对快速选择的优化，主要集中在分割点的选取上。

最左/最右作为分割点

这种就是我们通常随手实现的那种，性能几乎就是线性的，　也就是 O(n). 但是他解决不了已排序数组的问题，会退化到 O(n2).

随机选择分割点

由于我们的数组是未排序的，整个数组其实就是随机。因此这种方案与上面的方案本质上没什么区别，还是看运气。

三者中位数法选择分割点

取第一个，最后一个，中间位置，三个元素的中位数作为分割点。这样对已部分排序的数据依然能够达到线性复杂度。但是在人为构造的特殊数组上，还是会退化成 O(n2).

我猜想的算法思路：之所以随机选择法，会出现最坏的情况，是因为每次都选择到了最差也就是最大的数字。加入三个数字的中位数，可以保证选择到的分割点既不是最大，也不是最小，刻意避免了最坏的情况出现.

中位数的中位数法（又叫做 BFPRT 法，根据 5 个作者的名字首字母命名）

一次分割点的选择方法：

  1. 将所有元素分成 5 个一堆的组。获得了 (n/5) 个 5 元组。
  2. 每个 5 元组，通过插入排序的办法，求到中位数。
  3. 对于 (n/5) 个中位数，递归调用本方法，求到中位数。

时间复杂度分析

2021-03-25-21-19-49

为什么是 5??

1
2
3
4
5
6
7
在 BFPRT 算法中，为什么是选 5 个作为分组？

首先，偶数排除，因为对于奇数来说，中位数更容易计算。

如果选用 3，带入上面的公式，会发现和本身没有什么区别。

如果选取 7，9 或者更大，在插入排序时耗时增加，常数 [公式] 会很大，有些得不偿失。

实际应用

根据上面的原理，大概能得出的结论：

  • 三者中位数法，能提供不错的线性复杂度，但是有极小的概率遇到极端情况，导致 O(n2)
  • 中位数的中位数法，能提供绝对的线性时间复杂度保证。但是他的常数比较大，有时候有些浪费。

那么实际应用中当然是取长补短了。

所以实际应用中的最佳快速选择实现，应该是使用三者中位数法选取分割点，设置阈值，如果遇到了极端情况，切换到中位数的中位数 (BFPTR) 来保证最坏情况下的时间复杂度

真巧呢，Lucene 就是这么实现的。（不然我为啥会写呢？)

Lucene 源码org.apache.lucene.util.IntroSelector.

版本 8.7.0

定义

该类是一个抽象类，它只负责提供快速选择的分割点选择，左右分区, 不负责具体的存储介质，交换算法等。因此它有三个抽象方法，等待子类实现。

  • void swap(int i, int j): 交换算法，交换 i,j 两个下标的值
  • void setPivot(int i): 将 i 下标设置为分割点
  • int comparePivot(int j): 将 j 下标上的值与分割点进行比较，返回大小。

这三个方法和快速选择的精髓毫无关系，但是为了方便理解，这里给出一个简单的实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
  /**
 * 这是一个简单的，基于 int 数组的快速选择的实现
 */
public static class TestSelector extends IntroSelector{
    Integer[] actual;
    Integer pivot;

    public TestSelector(Integer[] actual) {
      this.actual = actual;
    }

    @Override
    protected void swap(int i, int j) {
      ArrayUtil.swap(actual, i, j);
    }

    @Override
    protected void setPivot(int i) {
      pivot = actual[i];
    }

    @Override
    protected int comparePivot(int j) {
      return pivot.compareTo(actual[j]);
    }
  }

核心 select 方法

1
2
3
4
5
6
public final void select(int from, int to, int k) {
    checkArgs(from, to, k);
// 递归的最大深度
    final int maxDepth = 2 * MathUtil.log(to - from, 2);
    quickSelect(from, to, k, maxDepth);
    }

核心方法比较简单，入参分别是：左下标，右下标，待寻找的 K.

  1. 检查参数
  2. 定义递归的最大深度
  3. 调用快速选择

什么是递归的最大深度

在原理部分讲到，实际应用时，使用三者中位数来进行快速选择，但是如果递归太多次，会认为遇到了极端情况，会切换到中位数的中位数
来进行分割点的选择。这里定义的阈值是：`递归深度　> 2*lg(n).

quickSelect

明显可以看出来，这里的 quick 不是快速选择的中名词（整个类才是真的快速选择)，而是一个形容词，形容是比较快的选择，那么就是三者中位数方法的快速选择实现了。

他的流程图如：

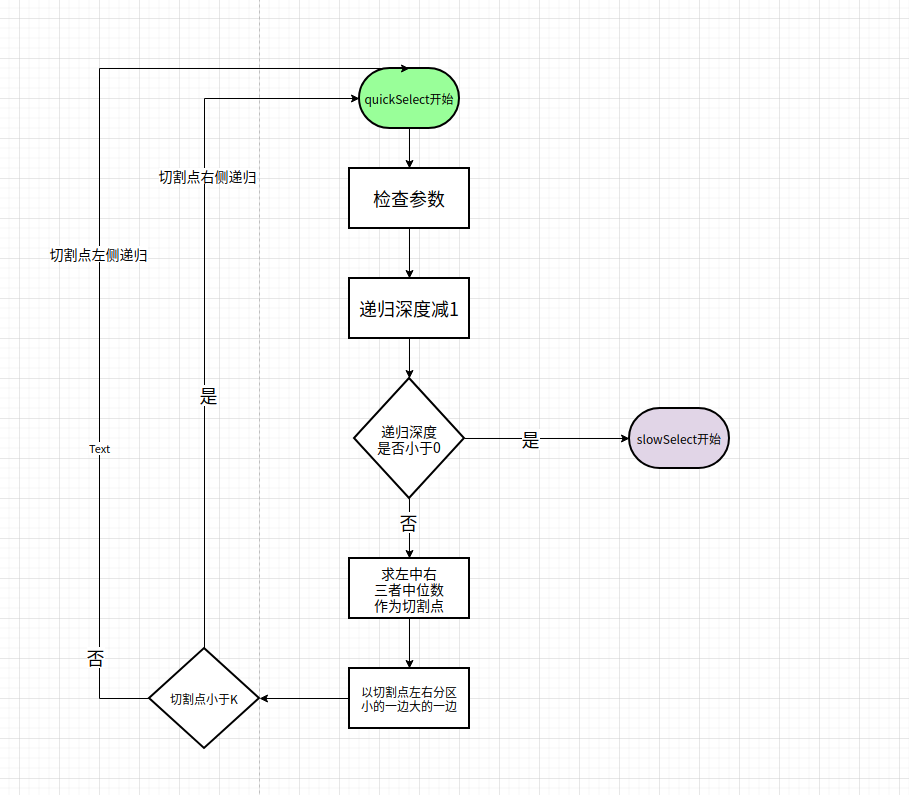
2021-03-25-22-00-02

结合代码中的注释，应该比较好懂。

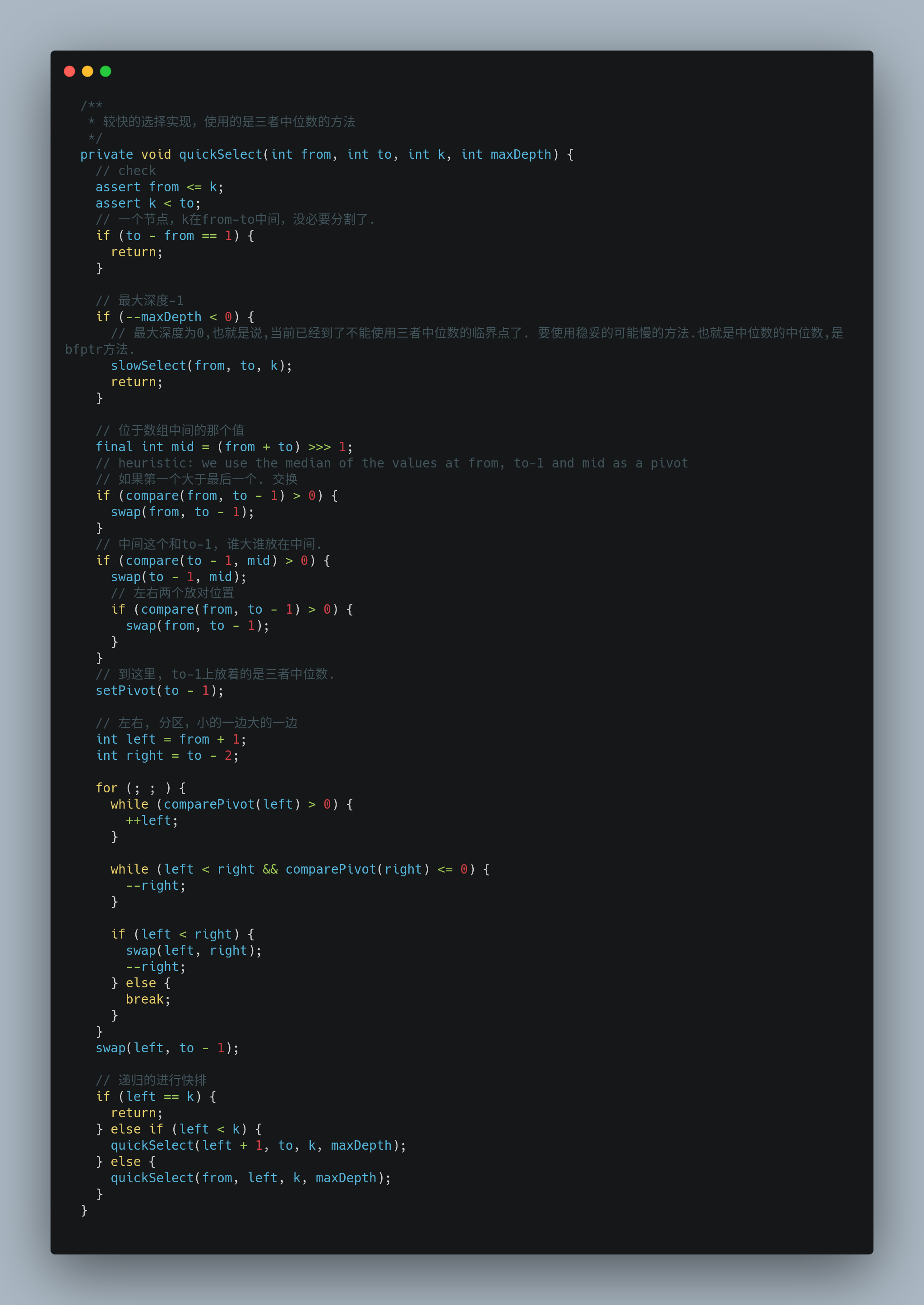
2021-03-25-22-41-37

核心逻辑可以概括为：

  1. 通过三者中位数求分割点
  2. 根据分割点左右分区移动数据
  3. 左右两边挑选 k 在的一边进行递归

插入一个逻辑是：如果每次开始时发现递归次数达到限制了，就走slowSelect.

slowSelect 方法

很明显，作者认为这个方法是较慢的，而上一个是较快的。这与我们学到的理论有点区别，我们学到的是数学证明的时间复杂度，这里的快慢更倾向于工业界的平均预估，对常量会比较敏感一点。

流程图：

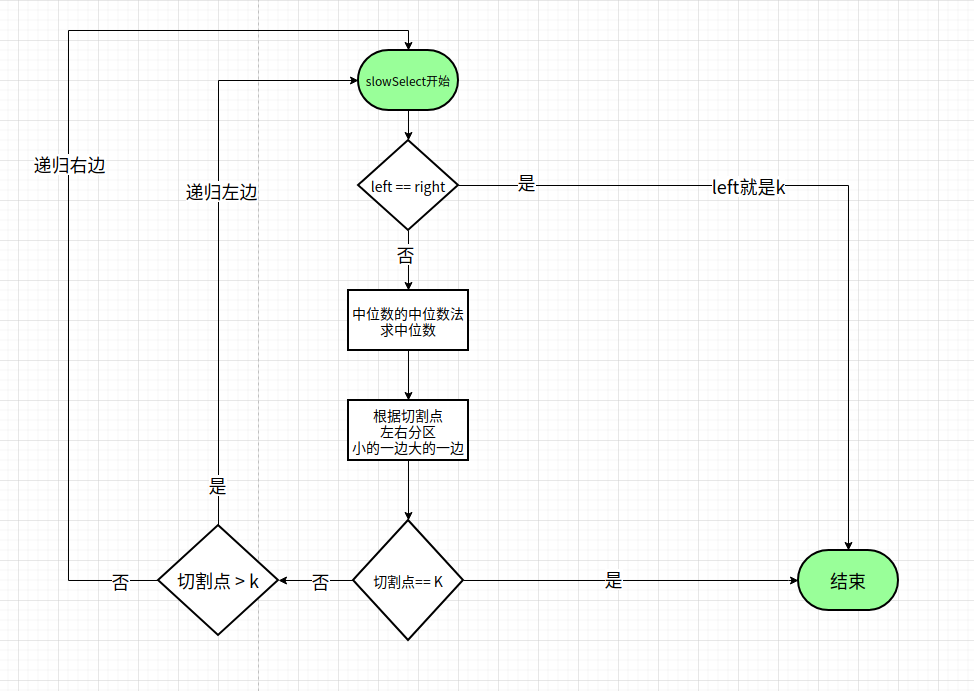
2021-03-25-22-29-57

代码：

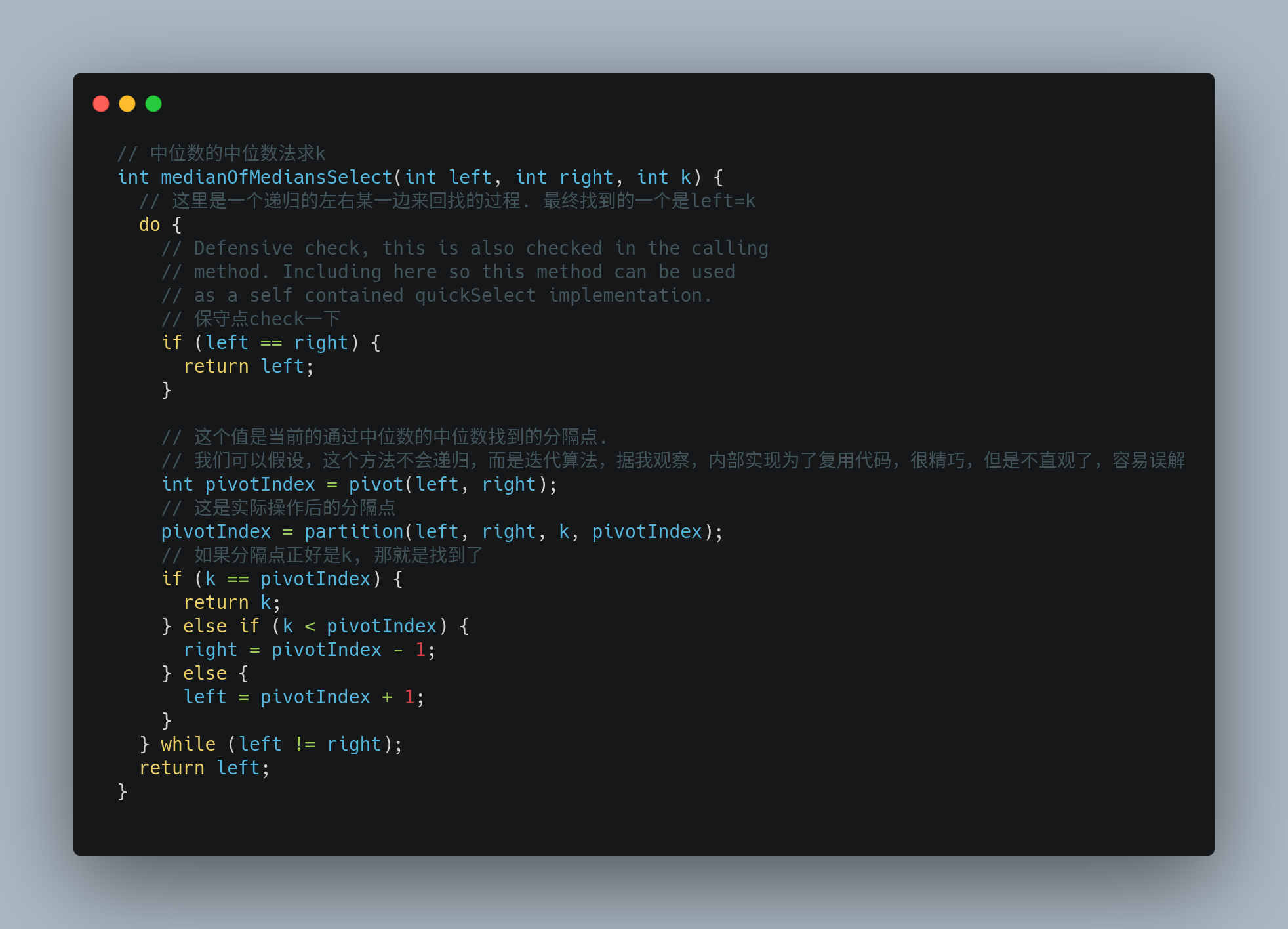
2021-03-25-22-41-03

核心逻辑：

  1. 左右相等则说明找到了，返回
  2. 用中位数的中位数法，求当前应该选择的分割点
  3. 根据分割点进行左右分区，小的一边，大的一边
  4. 根据分割点与 K 的大小，左右两边选择一边进行递归查找

其中用到了分区方法，没什么特别的，就是常见的快排分区方法，只是代码又是另一种风格，没必要贴出来。

pivot 方法

这个方法实现了对 [left,right]，求解中位数的中位数。

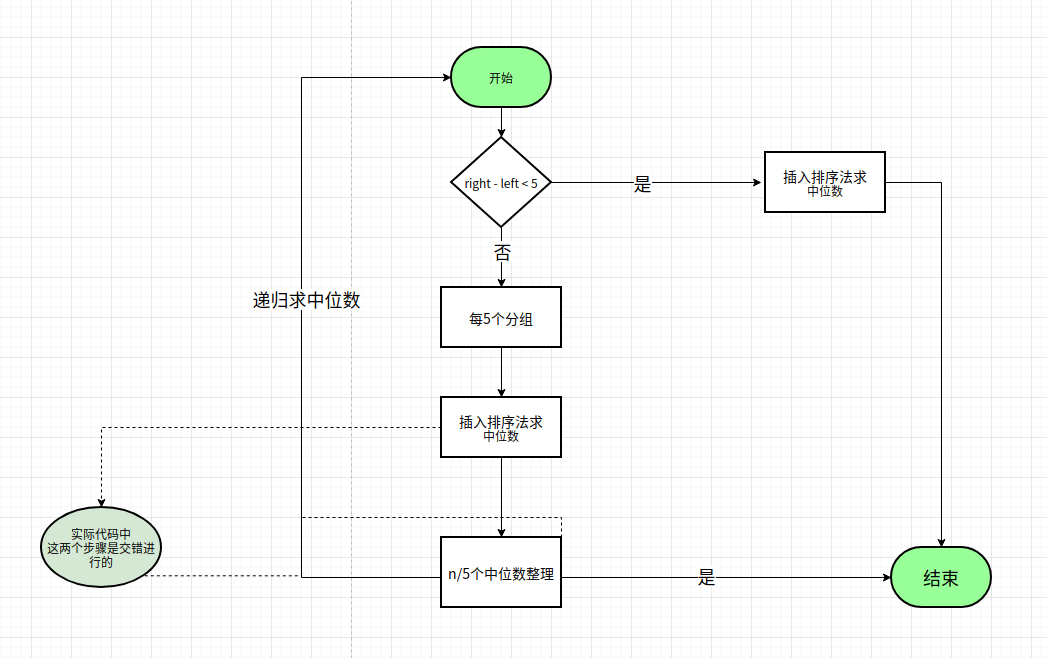
2021-03-25-22-34-19

这个所谓的中位数的中位数，理论上很好求解，又是一个递归的方法而已。为什么变复杂了呢？

想一下：

  • 快速选择的目的，是对一个未排序的数组，求第 k 大的元素。
  • 求中位数，是求数学上的中位数. 也是求未排序的数组中，求第length/2大的元素。

他们本质上讲是同构的，因此 Lucene 的代码中，为了复用代码，在求解中位数的中位数过程中，使用了部分slowSelect的代码，很是精巧，
但是对于刚看这份代码的人，会感到比较困惑。（是的，说的就是我自己，我也是写文章的时候才突然醒悟的）.

代码如下：

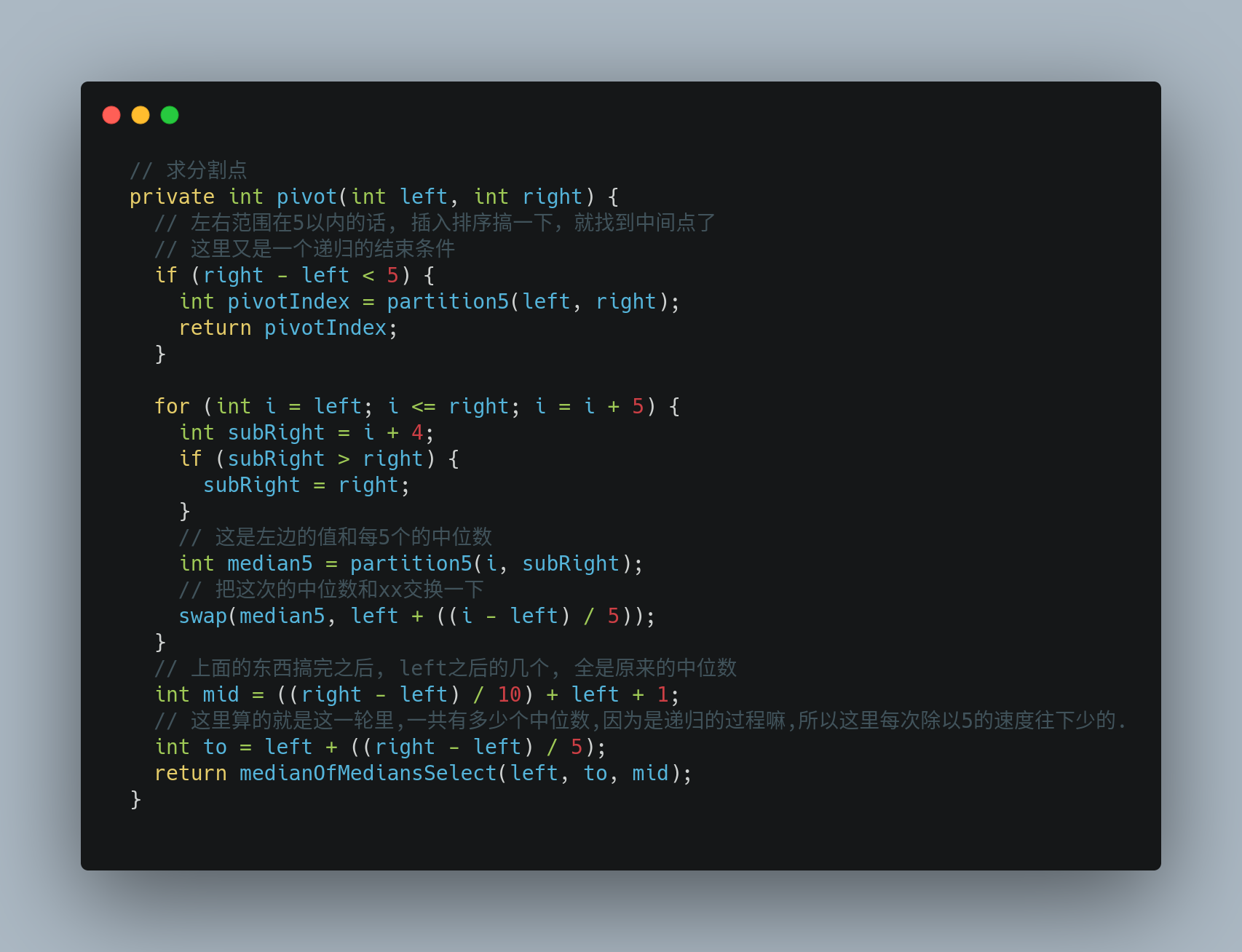
2021-03-25-22-40-20

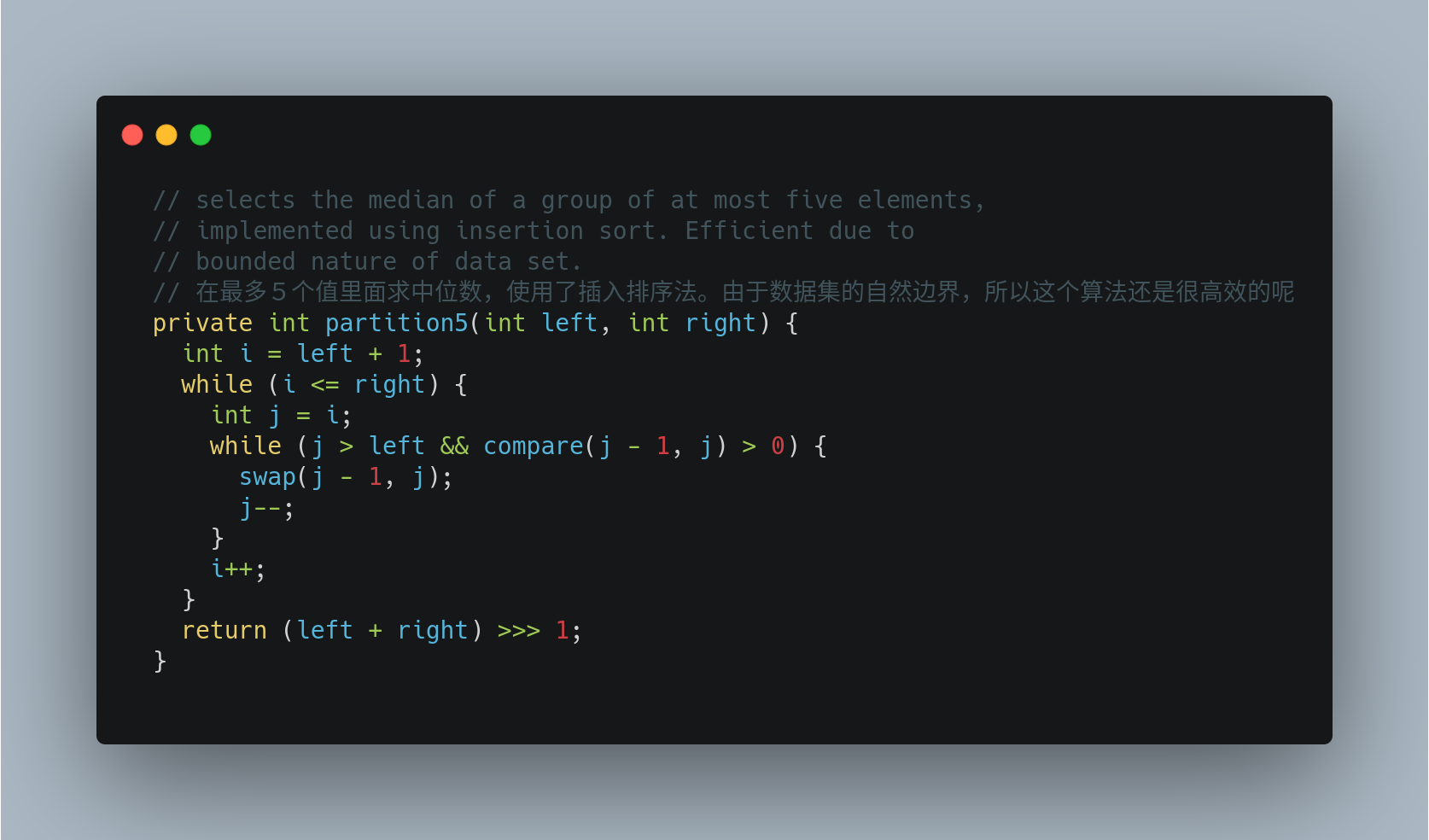
其中涉及到一个对 5 个以内的元素求中位数并且分区的方法，其实本质上就是直接进行了插入排序，然后取中位数。
因为控制了总数，所以插入排序的性能完全满足，且实现简单。

2021-03-25-22-43-49

总结

  1. 快速排序和快速选择，都是特别有用的，快排应用于大量的工业排序，快速选择应用于 topK 问题
  2. 快速排序和选择的核心，在于所谓主元（切割点）的选择
  3. 切割点的选择，有很多种优化方法，性能要求不高就随便写，性能要求高就按这篇文章讲的写。尽量使用三者中位数来求解切割点，注意防止极端情况，设置阈值使用中位数的中位数来求切割点即可。

说完了，有一说一。Lucene 的代码，精巧且难懂。但高效。

参考文章

https://zh.wikipedia.org/wiki/%E5%BF%AB%E9%80%9F%E9%80%89%E6%8B%A9

https://zhuanlan.zhihu.com/p/64627590


完。

联系我

最后，欢迎关注我的个人公众号【 呼延十 】，会不定期更新很多后端工程师的学习笔记。
也欢迎直接公众号私信或者邮箱联系我，一定知无不言，言无不尽。


以上皆为个人所思所得，如有错误欢迎评论区指正。

欢迎转载，烦请署名并保留原文链接。

联系邮箱：huyanshi2580@gmail.com

更多学习笔记见个人博客或关注微信公众号 < 呼延十 >——>呼延十

呼延十Developer

个人简介。